Solving Fizz Buzz with Cosines

Fizz Buzz is a counting game that has become oddly popular in the world of computer programming as a simple test of basic programming skills. The rules of the game are straightforward. Players say the numbers aloud in order beginning with one. Whenever a number is divisible by 3, they say 'Fizz' instead. If it is divisible by 5, they say 'Buzz'. If it is divisible by both 3 and 5, the player says both 'Fizz' and 'Buzz'. Here is a typical Python program that prints this sequence:

for n in range(1, 101):
    if n % 15 == 0:
        print('FizzBuzz')
    elif n % 3 == 0:
        print('Fizz')
    elif n % 5 == 0:
        print('Buzz')
    else:
        print(n)

Here is the output: fizz-buzz.txt. Can we make the program more complicated? The words 'Fizz', 'Buzz' and 'FizzBuzz' repeat in a periodic manner throughout the sequence. What else is periodic? Trigonometric functions! Perhaps we can use trigonometric functions to encode all four rules of the sequence in a single closed-form expression. That is what we are going to explore in this article. By the end, we will obtain a discrete Fourier series that can take any integer \( n \) and select the corresponding text to be printed.

Contents

• Definitions
  • Symbol Functions
  • Fizz Buzz Sequence
• Indicator Functions
• Complex Exponentials
• Cosines
• Discrete Fourier Transform
• Conclusion

Definitions

Before going any further, we establish a precise mathematical definition for the Fizz Buzz sequence. We begin by introducing a few functions that will help us define the Fizz Buzz sequence later.

Symbol Functions

We define a set of four functions \( \{ s_0, s_1, s_2, s_3 \} \) for integers \( n \) by: \begin{align*} s_0(n) &= n, \\ s_1(n) &= \mathtt{Fizz}, \\ s_2(n) &= \mathtt{Buzz}, \\ s_3(n) &= \mathtt{FizzBuzz}. \end{align*} We call these the symbol functions because they produce every term that appears in the Fizz Buzz sequence. The symbol function \( s_0 \) returns \( n \) itself. The functions \( s_1, \) \( s_2 \) and \( s_3 \) are constant functions that always return the literal words \( \mathtt{Fizz}, \) \( \mathtt{Buzz} \) and \( \mathtt{FizzBuzz} \) respectively, no matter what the value of \( n \) is.

Fizz Buzz Sequence

Now we can define the Fizz Buzz sequence as the sequence \[ (s_{f(n)}(n))_{n = 1}^{\infty} \] where \[ f(n) = \begin{cases} 1 & \text{if } 3 \mid n \text{ and } 5 \nmid n, \\ 2 & \text{if } 3 \nmid n \text{ and } 5 \mid n, \\ 3 & \text{if } 3 \mid n \text{ and } 5 \mid n, \\ 0 & \text{otherwise}. \end{cases} \] The notation \( m \mid n \) means that the integer \( m \) divides the integer \( n, \) i.e. \( n \) is a multiple of \( m. \) Equivalently, there exists an integer \( c \) such that \( n = cm . \) Similarly, \( m \nmid n \) means that \( m \) does not divide \( n, \) i.e. \( n \) is not a multiple of \( m. \) With the above definitions in place, we can expand the first few terms of the sequence explicitly as follows: \begin{align*} (s_{f(n)}(n))_{n = 1}^{\infty} &= (s_{f(1)}(1), \; s_{f(2)}(2), \; s_{f(3)}(3), \; s_{f(4)}(4), \; s_{f(5)}(5), \; s_{f(6)}(6), \; s_{f(7)}(7), \; \dots) \\ &= (s_0(1), \; s_0(2), \; s_1(3), \; s_0(4), s_2(5), \; s_1(6), \; s_0(7), \; \dots) \\ &= (1, \; 2, \; \mathtt{Fizz}, \; 4, \; \mathtt{Buzz}, \; \mathtt{Fizz}, \; 7, \; \dots). \end{align*} Note how the function \( f(n) \) produces an index \( i \) which we then use to select the symbol function \( s_i(n) \) to produce the \( n \)th term of the sequence. We therefore call \( f(n) \) the index function.

Indicator Functions

Here is the index function \( f(n) \) from the previous section with its cases and conditions rearranged to make it easier to spot interesting patterns: \[ f(n) = \begin{cases} 0 & \text{if } 5 \nmid n \text{ and } 3 \nmid n, \\ 1 & \text{if } 5 \nmid n \text{ and } 3 \mid n, \\ 2 & \text{if } 5 \mid n \text{ and } 3 \nmid n, \\ 3 & \text{if } 5 \mid n \text{ and } 3 \mid n. \end{cases} \] This function helps us to select another function \( s_{f(n)}(n) \) which in turn determines the \( n \)th term of the Fizz Buzz sequence. Our goal now is to replace this piecewise formula with a single closed-form expression. To do so, we first define indicator functions \( I_m(n) \) as follows: \[ I_m(n) = \begin{cases} 1 & \text{if } m \mid n, \\ 0 & \text{if } m \nmid n. \end{cases} \] The formula for \( f(n) \) can now be written as: \[ f(n) = \begin{cases} 0 & \text{if } I_5(n) = 0 \text{ and } I_3(n) = 0, \\ 1 & \text{if } I_5(n) = 0 \text{ and } I_3(n) = 1, \\ 2 & \text{if } I_5(n) = 1 \text{ and } I_3(n) = 0, \\ 3 & \text{if } I_5(n) = 1 \text{ and } I_3(n) = 1. \end{cases} \] Do you see a pattern? Here is the same function written as a table:

Do you see it now? If we treat the values in the first two columns as binary digits and the values in the third column as decimal numbers, then in each row the first two columns give the binary representation of the number in the third column. For example, \( 3_{10} = 11_2 \) and indeed in the last row of the table, we see the bits \( 1 \) and \( 1 \) in the first two columns and the number \( 3 \) in the last column. In other words, writing the binary digits \( I_5(n) \) and \( I_3(n) \) side by side gives us the binary representation of \( f(n). \) Therefore \[ f(n) = 2 \, I_5(n) + I_3(n). \] We can now write a small program to demonstrate this formula:

for n in range(1, 101):
    s = [n, 'Fizz', 'Buzz', 'FizzBuzz']
    i = (n % 3 == 0) + 2 * (n % 5 == 0)
    print(s[i])

We can make it even shorter at the cost of some clarity:

for n in range(1, 101):
    print([n, 'Fizz', 'Buzz', 'FizzBuzz'][(n % 3 == 0) + 2 * (n % 5 == 0)])

What we have obtained so far is pretty good. While there is no universal definition of a closed-form expression, I think most people would agree that the indicator functions as defined above are simple enough to be permitted in a closed-form expression.

Complex Exponentials

In the previous section, we obtained the formula \[ f(n) = I_3(n) + 2 \, I_5(n) \] which we then used as an index to look up the text to be printed. We also argued that this is a pretty good closed-form expression already.

However, in the interest of making things more complicated, we must ask ourselves: What if we are not allowed to use the indicator functions? What if we must adhere to the commonly accepted meaning of a closed-form expression which allows only finite combinations of basic operations such as addition, subtraction, multiplication, division, integer exponents and roots with integer index as well as functions such as exponentials, logarithms and trigonometric functions. It turns out that the above formula can be rewritten using only addition, multiplication, division and the cosine function. Let us begin the translation. Consider the sum \[ S_m(n) = \sum_{k = 0}^{m - 1} e^{2 \pi i k n / m}, \] where \( i \) is the imaginary unit and \( n \) and \( m \) are integers. This is a geometric series in the complex plane with ratio \( r = e^{2 \pi i n / m}. \) If \( n \) is a multiple of \( m , \) then \( n = cm \) for some integer \( c \) and we get \[ r = e^{2 \pi i n / m} = e^{2 \pi i c} = 1. \] Therefore, when \( n \) is a multiple of \( m, \) we get \[ S_m(n) = \sum_{k = 0}^{m - 1} e^{2 \pi i k n / m} = \sum_{k = 0}^{m - 1} 1^k = m. \] If \( n \) is not a multiple of \( m, \) then \( r \ne 1 \) and the geometric series becomes \[ S_m(n) = \frac{r^m - 1}{r - 1} = \frac{e^{2 \pi i n} - 1}{e^{2 \pi i n / m} - 1} = 0. \] Therefore, \[ S_m(n) = \begin{cases} m & \text{if } m \mid n, \\ 0 & \text{if } m \nmid n. \end{cases} \] Dividing both sides by \( m, \) we get \[ \frac{S_m(n)}{m} = \begin{cases} 1 & \text{if } m \mid n, \\ 0 & \text{if } m \nmid n. \end{cases} \] But the right-hand side is \( I_m(n). \) Therefore \[ I_m(n) = \frac{S_m(n)}{m} = \frac{1}{m} \sum_{k = 0}^{m - 1} e^{2 \pi i k n / m}. \]

Cosines

We begin with Euler's formula \[ e^{i x} = \cos x + i \sin x \] where \( x \) is a real number. From this formula, we get \[ e^{i x} + e^{-i x} = 2 \cos x. \] Therefore \begin{align*} I_3(n) &= \frac{1}{3} \sum_{k = 0}^2 e^{2 \pi i k n / 3} \\ &= \frac{1}{3} \left( 1 + e^{2 \pi i n / 3} + e^{4 \pi i n / 3} \right) \\ &= \frac{1}{3} \left( 1 + e^{2 \pi i n / 3} + e^{-2 \pi i n / 3} \right) \\ &= \frac{1}{3} + \frac{2}{3} \cos \left( \frac{2 \pi n}{3} \right). \end{align*} The third equality above follows from the fact that \( e^{4 \pi i n / 3} = e^{6 \pi i n / 3} e^{-2 \pi i n / 3} = e^{2 \pi i n} e^{-2 \pi i n/3} = e^{-2 \pi i n / 3}. \)

The function above is defined for integer values of \( n \) but we can extend its formula to real \( x \) and plot it to observe its shape between integers. As expected, the function takes the value \( 1 \) whenever \( x \) is an integer multiple of \( 3 \) and \( 0 \) whenever \( x \) is an integer not divisible by \( 3. \)

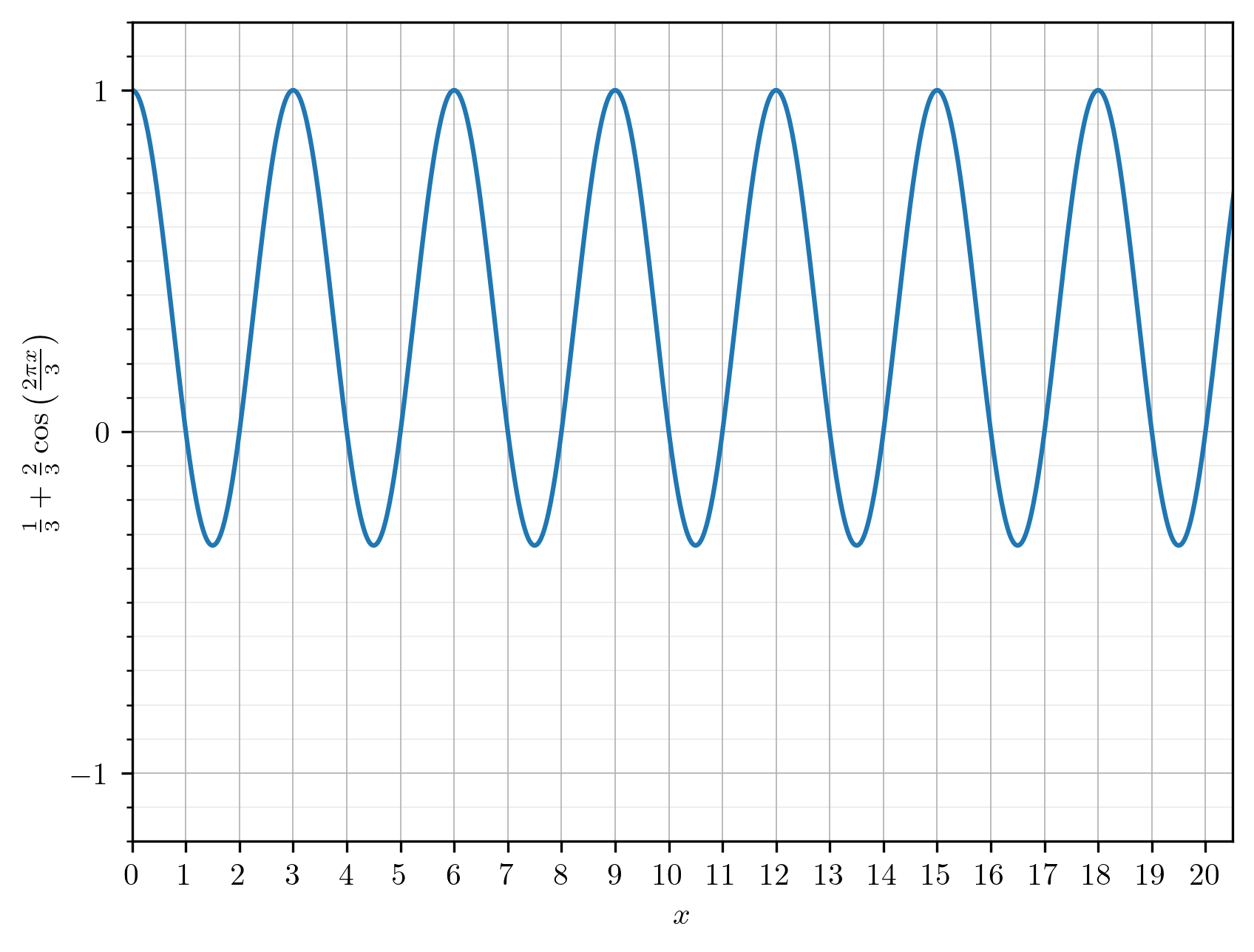
Similarly, \begin{align*} I_5(n) &= \frac{1}{5} \sum_{k = 0}^4 e^{2 \pi i k n / 5} \\ &= \frac{1}{5} \left( 1 + e^{2 \pi i n / 5} + e^{4 \pi i n / 5} + e^{6 \pi i n / 5} + e^{8 \pi i n / 5} \right) \\ &= \frac{1}{5} \left( 1 + e^{2 \pi i n / 5} + e^{4 \pi i n / 5} + e^{-4 \pi i n / 5} + e^{-2 \pi i n / 5} \right) \\ &= \frac{1}{5} + \frac{2}{5} \cos \left( \frac{2 \pi n}{5} \right) + \frac{2}{5} \cos \left( \frac{4 \pi n}{5} \right). \end{align*} Extending this expression to real values of \( x \) allows us to plot its shape as well. Once again, the function takes the value \( 1 \) at integer multiples of \( 5 \) and \( 0 \) at integers not divisible by \( 5. \)

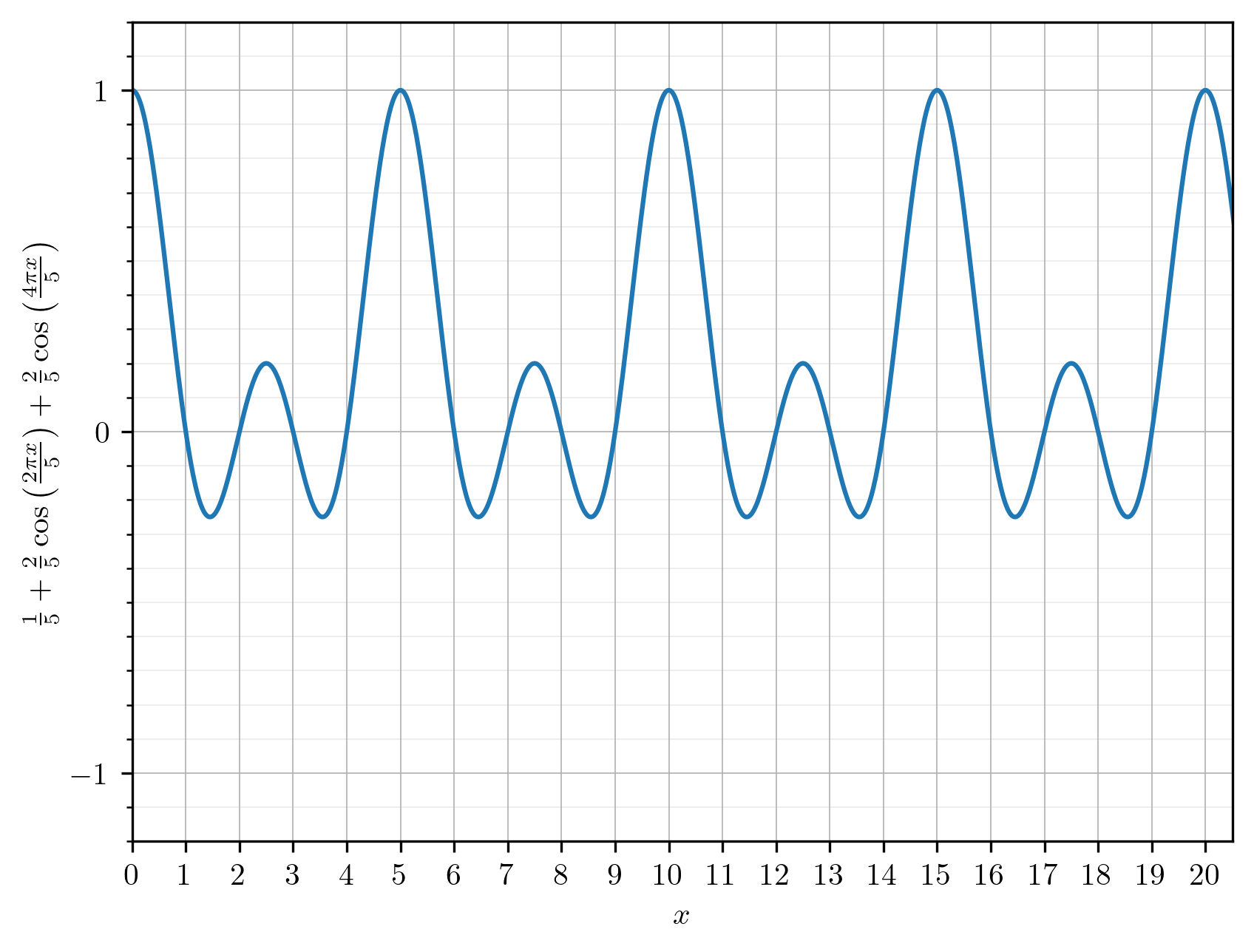
Recall that we expressed \( f(n) \) as \[ f(n) = I_3(n) + 2 \, I_5(n). \] Substituting these trigonometric expressions yields \[ f(n) = \frac{1}{3} + \frac{2}{3} \cos \left( \frac{2 \pi n}{3} \right) + 2 \cdot \left( \frac{1}{5} + \frac{2}{5} \cos \left( \frac{2 \pi n}{5} \right) + \frac{2}{5} \cos \left( \frac{4 \pi n}{5} \right) \right). \] A straightforward simplification gives \[ f(n) = \frac{11}{15} + \frac{2}{3} \cos \left( \frac{2 \pi n}{3} \right) + \frac{4}{5} \cos \left( \frac{2 \pi n}{5} \right) + \frac{4}{5} \cos \left( \frac{4 \pi n}{5} \right). \] We can extend this expression to real \( x \) and plot it as well. The resulting curve takes the values \( 0, 1, 2 \) and \( 3 \) at integer points, as desired.

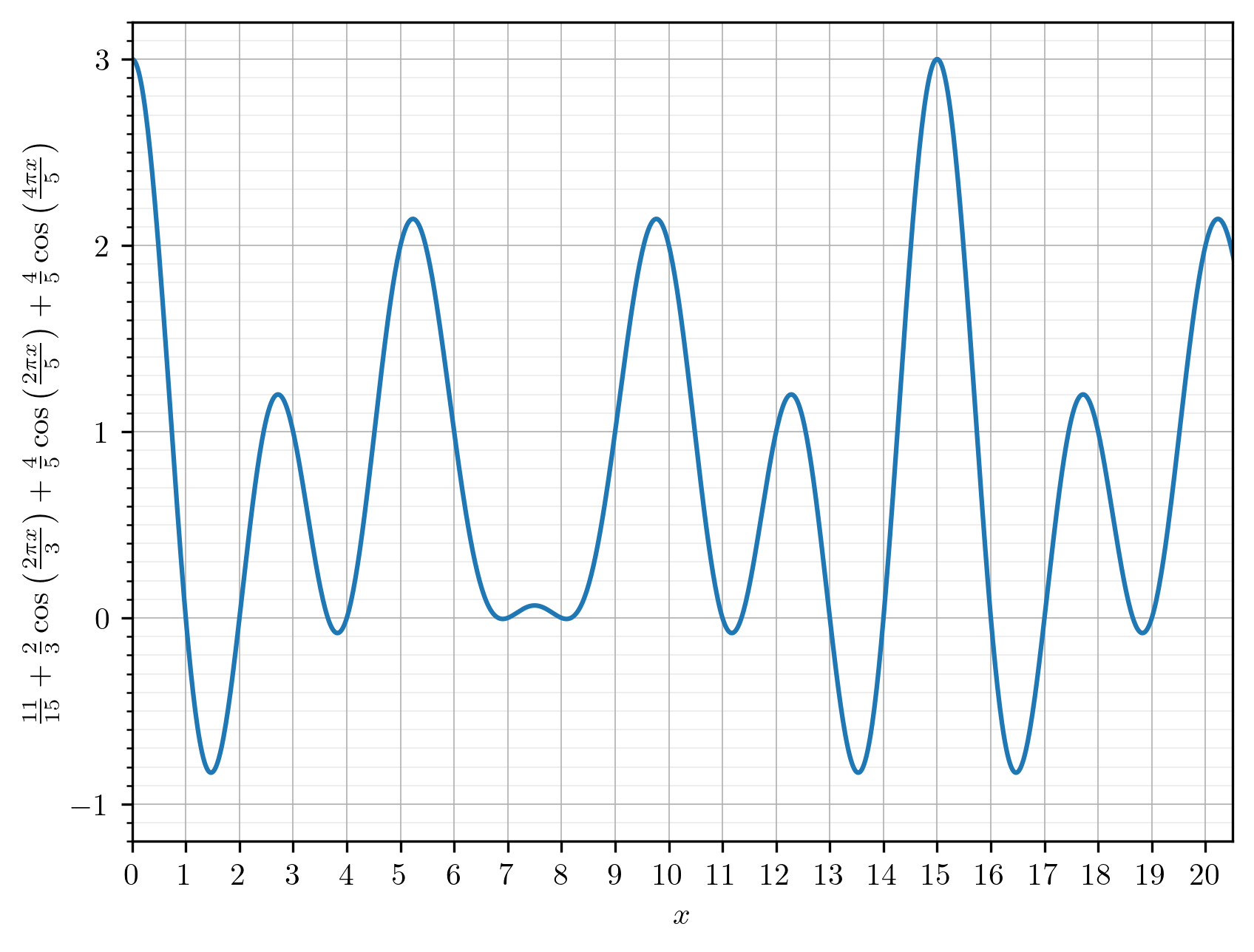
Now we can write our Python program as follows:

from math import cos, pi
for n in range(1, 101):
    s = [n, 'Fizz', 'Buzz', 'FizzBuzz']
    i = round(11 / 15 + (2 / 3) * cos(2 * pi * n / 3)
                      + (4 / 5) * cos(2 * pi * n / 5)
                      + (4 / 5) * cos(4 * pi * n / 5))
    print(s[i])

Discrete Fourier Transform

The keen-eyed might notice that the expression we obtained for \( f(n) \) is a finite Fourier series. This is not surprising, since the output of a Fizz Buzz programme depends only on \( n \bmod 15 . \) Any function on a finite cyclic group can be written exactly as a finite Fourier expansion. In this section, we recover the same function \( f(n) \) using the discrete Fourier transform. It is worth mentioning here that the calculations presented here are quite tedious to do by hand. Nevertheless, this section offers a glimpse of how such coefficients are calculated. By the end, we will arrive at exactly the same \( f(n) \) as before. There is nothing new to discover here. We simply obtain the result by a different, more direct and noticeably tedious method. If this doesn't sound interesting to you, you may safely skip this section.

We know that \( f(n) \) is a periodic function with period \( 15. \) To apply the discrete Fourier transform, we look at one complete period using the indices \( n = 1, 2, \dots, 15. \) Over this period, the values are: \begin{array}{c|ccccccccccccccc} n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 \\ \hline f(n) & 0 & 0 & 1 & 0 & 2 & 1 & 0 & 0 & 1 & 2 & 0 & 1 & 0 & 0 & 3 \end{array} The discrete Fourier transform gives us the constants defined by: \[ c_k = \frac{1}{15} \sum_{n = 1}^{15} f(n) e^{-2 \pi i k n / 15}, \] for \( k = 1, 2, \dots, 15. \) These constants reconstruct \( f(n) \) via the inverse transform: \[ f(n) = \sum_{k = 1}^{15} c_k e^{2 \pi i k n / 15} \] where \( n \in \mathbb{Z}. \) Let us compute the first constant: \[ c_1 = \frac{1}{15}\left( \begin{aligned} e^{-2 \pi i \cdot 3/15} &+ 2 e^{-2 \pi i \cdot 5/15} + e^{-2 \pi i \cdot 6/15} + e^{-2 \pi i \cdot 9/15} \\ &+ 2 e^{-2 \pi i \cdot 10/15} + e^{-2 \pi i \cdot 12/15} + 3 e^{-2 \pi i \cdot 15/15} \end{aligned} \right) = 0. \] Similarly, \[ c_2 = \frac{1}{15}\left( \begin{aligned} e^{-2 \pi i \cdot 6/15} &+ 2 e^{-2 \pi i \cdot 10/15} + e^{-2 \pi i \cdot 12/15} + e^{-2 \pi i \cdot 18/15} \\ &+ 2 e^{-2 \pi i \cdot 20/15} + e^{-2 \pi i \cdot 24/15} + 3 e^{-2 \pi i \cdot 30/15} \end{aligned} \right) = 0. \] and \[ c_3 = \frac{1}{15}\left( \begin{aligned} e^{-2 \pi i \cdot 9/15} &+ 2 e^{-2 \pi i \cdot 15/15} + e^{-2 \pi i \cdot 18/15} + e^{-2 \pi i \cdot 27/15} \\ &+ 2 e^{-2 \pi i \cdot 30/15} + e^{-2 \pi i \cdot 36/15} + 3 e^{-2 \pi i \cdot 45/15} \end{aligned} \right) = \frac{2}{5}. \] Continuing in this manner, we find all the constants: \begin{align*} c_1 &= c_2 = c_4 = c_7 = c_8 = c_{11} = c_{13} = c_{14} = 0, \\ c_3 &= c_6 = c_9 = c_{12} = \frac{2}{5}, \\ c_5 &= c_{10} = \frac{1}{3}, \\ c_{15} &= \frac{11}{15}. \end{align*} Using the inverse transform, we get \begin{align*} f(n) &= \sum_{k = 1}^{15} c_k \, e^{2 \pi i k n / 15} \\ &= \frac{11}{15} + \frac{2}{5} \left( e^{2 \pi i \cdot 3n/15} + e^{2 \pi i \cdot 6n/15} + e^{2 \pi i \cdot 9n/15} + e^{2 \pi i \cdot 12n/15} \right) \\ &\phantom{=} \phantom{\frac{11}{15}} + \frac{1}{3} \left( e^{2 \pi i \cdot 5n/15} + e^{2 \pi i \cdot 10n/15} \right) \\ &= \frac{11}{15} + \frac{2}{5} \left( e^{6 \pi i n/15} + e^{12 \pi i n/15} + e^{18 \pi i n/15} + e^{24 \pi i n/15} \right) \\ &\phantom{=} \phantom{\frac{11}{15}} + \frac{1}{3} \left( e^{10 \pi i n/15} + e^{20 \pi i n/15} \right) \\ &= \frac{11}{15} + \frac{2}{5} \left( e^{6 \pi i n/15} + e^{12 \pi i n/15} + e^{-12 \pi i n/15} + e^{-6 \pi i n/15} \right) \\ &\phantom{=} \phantom{\frac{11}{15}} + \frac{1}{3} \left( e^{10 \pi i n/15} + e^{-10 \pi i n/15} \right) \\ &= \frac{11}{15} + \frac{2}{5} \left( 2 \cos \left( \frac{6 \pi n}{15} \right) + 2 \cos \left( \frac{12 \pi n}{15} \right) \right) \\ &\phantom{=} \phantom{\frac{11}{15}} + \frac{1}{3} \left( 2 \cos \left( \frac{10 \pi n}{15} \right) \right) \\ &= \frac{11}{15} + \frac{4}{5} \cos \left( \frac{2 \pi n}{5} \right) + \frac{4}{5} \cos \left( \frac{4 \pi n}{5} \right) + \frac{2}{3} \cos \left( \frac{2 \pi n}{3} \right). \end{align*} This gives us exactly the same function \( f(n) \) we obtained earlier. The difference is only in how we arrived there. Working out Fourier coefficients by hand is slow and mechanical. In practice these sums are almost always computed automatically by numerical software or computer algebra systems. Still, this exercise shows that our humble Fizz Buzz index function can be expressed precisely using the machinery of Fourier analysis.

Conclusion

To summarise, we have defined the Fizz Buzz sequence as \[ (s_{f(n)}(n))_{n = 1}^{\infty} \] where \[ f(n) = \frac{11}{15} + \frac{2}{3} \cos \left( \frac{2 \pi n}{3} \right) + \frac{4}{5} \cos \left( \frac{2 \pi n}{5} \right) + \frac{4}{5} \cos \left( \frac{4 \pi n}{5} \right). \] and \( s_0(n) = n, \) \( s_1(n) = \mathtt{Fizz}, \) \( s_2(n) = \mathtt{Buzz} \) and \( s_3(n) = \mathtt{FizzBuzz}. \) A Python program to print the Fizz Buzz sequence based on this definition was presented earlier. That program can be written more succinctly as follows:

from math import cos, pi
for n in range(1, 101):
    print([n, 'Fizz', 'Buzz', 'FizzBuzz'][round(11 / 15 + (2 / 3) * cos(2 * pi * n / 3) + (4 / 5) * (cos(2 * pi * n / 5) + cos(4 * pi * n / 5)))])

We can also wrap this up nicely in a shell one-liner, in case you want to share it with your friends and family and surprise them:

python3 -c 'from math import cos, pi; [print([n, "Fizz", "Buzz", "FizzBuzz"][round(11/15 + (2/3) * cos(2*pi*n/3) + (4/5) * (cos(2*pi*n/5) + cos(4*pi*n/5)))]) for n in range(1, 101)]'

We have taken a simple counting game and turned it into a trigonometric construction: a finite Fourier series with a constant term \( 11/15 \) and three cosine terms with coefficients \( 2/3, \) \( 4/5 \) and \( 4/5. \) None of this makes Fizz Buzz any easier, of course, but it does show that every \( \mathtt{Fizz} \) and \( \mathtt{Buzz} \) now owes its existence to a particular set of Fourier coefficients. We began with the modest goal of making this simple problem more complicated. I think it is safe to say that we did not fall short.